Capacity Reduction of a Compression Member with an Initial Deformation
A recent review of equipment installed in a power plant found a piping strut that was visibly bent. Would the bend in the strut reduce its load bearing capacity as a compression member?
The answer is YES! The load bearing capacity of a bent strut against buckling is reduced. The reduction in buckling capacity is a function of the strut’s section properties and its initial deformation. We will see here how this can be quantified analytically (closed-form solution) and numerically (FEA solution).
The equation for the maximum axial load capacity of a column, before it buckles, was first formulated by Leonhard Euler in 1757.
Fcr = (π2 E I)/(K L)2
Where E = Young’s modulus of column material; I = cross-sectional moment of inertia of the column; L = unbraced length of column; and K is a factor that depends on the degree of fixity in the ends. For example, K = 1 for free ends, and 0.5 for fixed ends.
This equation is still in widespread use today, and forms the basis of current design standards for evaluation of members in compression. While the steel design codes use the same underlying methodology, they vary in their margin of safety, which is included either as factors on the terms in the Euler equation or as compressive stress limits. For example, ASME provides methods for evaluation of column buckling in ASME (2015) III Appendix F-1334.5 and Appendix NF-3322.1.c.1. AISC provides a method in Steel Construction Manual (2005) Chapters E and H. All of these methods determine an allowable axial load (or stress) based on the Euler formula, then compare to an interaction ratio limit for combined axial plus bending.
Since these methods consider the combined effects of axial and bending load, for the bent strut, we could include the bending moment calculated from the axial force multiplied by the offset. However, a more accurate method is to use an equation that includes both the initial and the progressive effects of the offset. This method is found by deriving a general solution. Beginning with the Euler beam theory that is the basis for the column buckling formula shown above:
M = -E I (d2 ω)/(dx2 )
Where w(x) is the deformed shape of the strut, and the other terms are as defined above. The second derivative term is the slope of the beam at any given point. To calculate the slope, approximate the bend in the strut as a half sine wave with a given amplitude. Thus, the maximum stress in the bent strut, with an initial eccentricity is:
σmax=Faxial (1/A+(ecc R)/I sec(π/2 √(Faxial/Fcr )) )
Where A = cross-sectional area of the column (strut); ecc = initial eccentricity; R = radius of the cylindrical column; Faxial = applied axial load; and Fcr = axial load calculated using the Euler formula.
Thus, the bent strut can be evaluated using a closed-form solution. As an alternative evaluation method, the same problem can also be solved with a finite element model. Model the strut, using a FEA model, with an initial curvature and fully plastic material properties, then apply the maximum axial load that produces a stable solution.
Figure 1 – ANSYS model of strut with pinned ends (note: curvature too small to see)
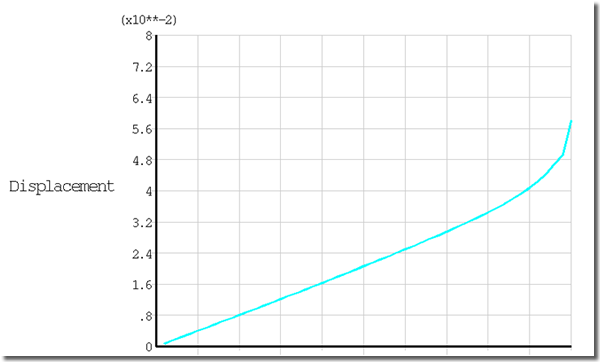Figure 2 – Displacement graph showing solution approaches stability limit
Since the strut is subject to both column buckling and progressive bending, the strut cannot develop the full critical Euler buckling load, but will instead fail at a lesser load when a plastic hinge occurs due to the bending caused by the progressive eccentricity. For the case of a 72 in. long, 3 in. diameter solid steel strut, with an initial deformation of 0.25 in. at center, the ANSYS model reveals that the plastic hinge occurs at approximately 50% of the Euler buckling capacity of an unbent strut. A comparable result can be found using the closed-form solution by choosing Faxial such the maximum stress is equal to the yield stress, as an estimate of plastic hinge initiation. The resulting closed-form solution is within ten percent of the finite element solution.
Very well explained! With the help of piping design model, the problem has been solved. The load bearing capacity of a bent strut against buckling is reduced.