Recent Advances in Becht’s HTHA Damage Modeling Approach Part 6: Nucleation Effects and Cutoff Pressure Prediction
Overview
We presented a comprehensive five part series on our HTHA modeling approach in the fall of 2020. This series extended the initial work presented in [1] in several significant ways, including:
- Inclusion of vessel pressure and weld residual stresses
- Treatment of C-0.5Mo material
- Direct relation of the damage and life fractions the model predicts to both microstructural damage and toughness loss
- Definition of a simple but predictive through-wall failure criterion
- Validation of through-wall damage predictions to almost 100 case histories
We have continued to progress and refine our HTHA model in the meantime, with a notable addition being incorporation of nucleation effects. Nucleation captures the fact that a certain driving force is needed to start a void growing, which means that there is a hydrogen partial pressure below which HTHA cannot initiate (called a cutoff pressure here). This blog introduces the classical model for nucleation, details how it is incorporated in the overall Becht HTHA model and finally presents revised time-based Nelson Curves appropriate for inclusion in [2].
Motivation
As shown and discussed in Part 1 of this blog series (Part 1, Figure 1), when there is applied (or “external”) stress there is no longer a pressure cutoff as hydrogen partial pressures approach zero; this physically represents simple creep failure in the given time for the given applied stress. This is easily seen in Figure 1 below where our predicted Nelson Curves diverge from the API RP 941 Nelson Curves when they go vertical. The creep failure represented in Figure 1 actually corresponds to pure iron (or ferrite) because those are the material properties used in the void growth model (to represent the carbon-depleted zone around actual HTHA voids). This is much too conservative for actual carbon steel in the absence of hydrogen, and so one option is simply to correct the 0-hydrogen temperatures to correspond to the failure temperature that API 579-1/ASME FFS-1 [3] or API RP 530 [4] would predict. After discussions with several industry experts, it was determined that simply removing creep failure from the Nelson Curves is the most consistent with the current curves in API RP 941. The simplest and most physical way to accomplish this is invoking nucleation concepts.
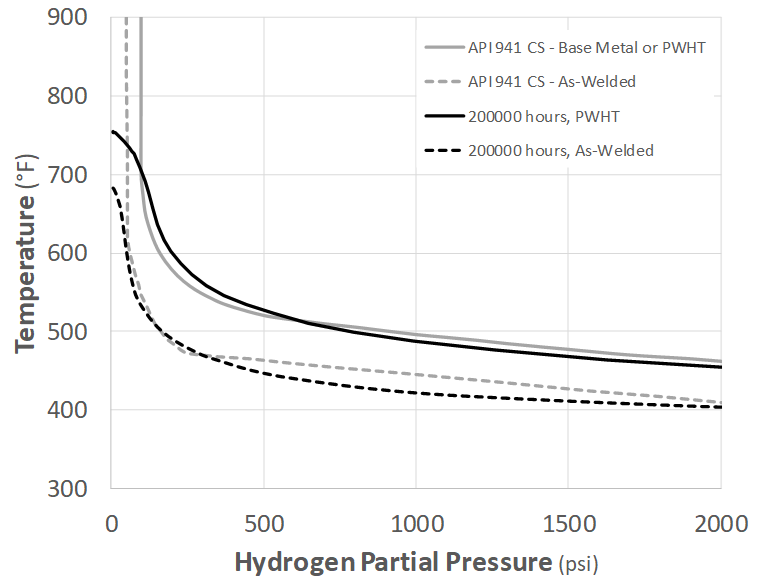
Figure 1 – Example of Predicted Nelson Curves Applied Stress Effect
Nucleation
The void growth models the Becht HTHA model is based on are also the models most used for considering nucleation of voids. This is important because quite simply if a void can’t nucleate, then it can’t grow and HTHA damage will be avoided. There is a standard term in the overall driving force expression often referred to as the sintering stress (σs):
σs = 2γ/r
One of the early works [5] showing this term is highlighted in Figure 2 where it can be seen that the sintering stress works against methane pressure and applied stress (from sources such as vessel internal pressure, weld residual stress or piping system loads). Note that the overall equation in Figure 2 is for void growth due to grain boundary diffusion (one of three terms used in modern void growth models) and is an extension from the work of [6]; Figure 2 repeats an error in [6] that was not corrected until later [7], and so is shown for illustration of concepts only.

Figure 2 – Void Growth Model Driving Force Including Nucleation (from [3])
The sintering stress physically represents surface tension (where g = 0.00195 N/mm is the surface tension coefficient for pure iron) working to pull the curved surfaces of the initial void flat. This stress scales with 1/r where r is the radius of this initial void. When the void is small, the sintering stress is large, and as the radius grows (if it grows) this terms eventually becomes negligible. In fact, this term is often neglected (which is the approach we also took). The sintering stress (=2γ/r) is plotted below in Figure 3 to illustrate this rapid drop-off with increasing void size.
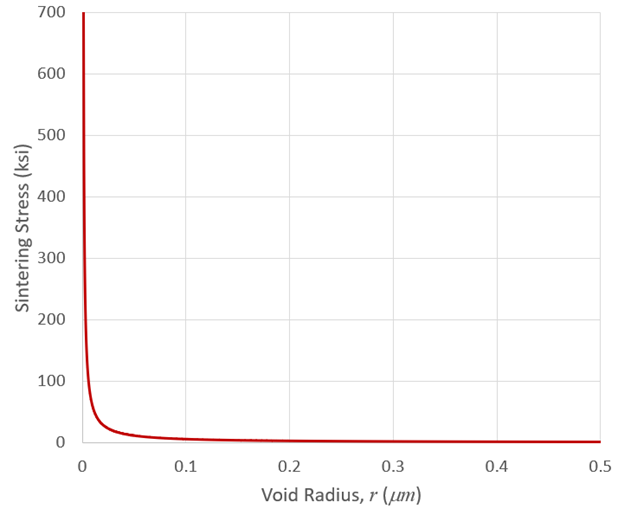
Figure 3 – Sintering Stress vs. Void Radius
For a void to grow then, the pressure inside the void and the applied stress working to open it must be larger than the sintering stress; otherwise the void may actually shrink in size. In equation form this is expressed as
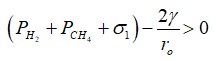
This expression can rearranged to give the smallest radius, ro, that can still grow for a given applied loading (methane pressure and stress).
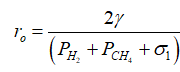
This radius is frequently referred to as the critical void radius. The question is, what is this value? We know that HTHA voids, even at failure, are on the order of a mm, so logically, the critical radius should be fractions of a mm. The impact of various critical radius choices on the predicted Nelson Curves for C-0.5Mo (PWHT, lower bound failure) are shown in Figure 4. As the assumed critical radius gets larger (which means the sintering stress gets smaller) there is eventually no impact on the predicted curve at all. Note that for simplicity (and with reference to Figure 3) the sintering stress is implemented as a simple threshhold in our model currently; if the methane pressure and applied stress are not greater than the critical sintering stress, then HTHA cannot proceed and the Nelson Curve is simply truncated (creating the purely vertical part of the curve).
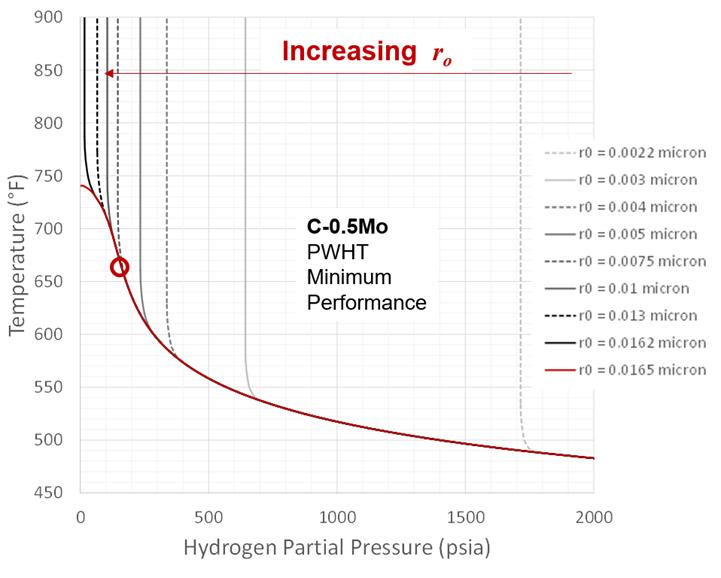
Figure 4 – Critical Radius Effect on Nelson Curves
With reference to Figure 4 again, the approximate inflection point of the baseline curve (where it begins to turn back toward to temperature axis) is circled; this value corresponds almost exactly with a critical radius of 0.0075 mm (microns). This inflection point is essentially the point where pure creep begins to dominate over HTHA and seems a reasonable point to truncate the curves. In fact, a critical radius of approximately 0.0075 mm lines up with predicted Nelson Curve inflection points in our model across a huge span of times, materials (carbon steel, C-0.5Mo) and conditions (PWHT, as-welded).
Interestingly, this critical radius corresponds to a threshold sintering stress of:
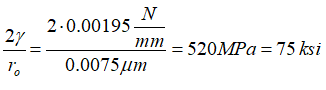
Which is on the order of the ultimate tensile strength for the materials in question as well. With this mind, a single value of critical radius (0.0075 mm) gives a simple and physically reasonable value for an HTHA threshold that can be used across materials, conditions, times and process conditions.
Updated Nelson Curves
The Nelson Curves from Part 5 are updated here to incorporate a driving force threshold of 75 ksi into the model prediction. As before the curves correspond to “failure” (100 % damage to 25% wall depth as described in previous blog parts). To highlight the basic difference that a nucleation threshold makes, 200,000 hour results for a typical carbon steel (SA-106 Gr. B) are compared to the existing API RP 941 curves with excellent agreement – including now in the vertical portion of the curves. This general agreement with existing practice for a reasonable time choice (200,000 hours) again reinforces the reasonableness of the model predictions.
The updated Carbon Steel time-based Nelson Curves are shown in Figure 6 and Figure 7 – recall these curves conservatively correspond to SA-516 Gr. 70. The updated C-0.5Mo curves (conservatively corresponding to SA-204 Gr. C) are shown in Figure 8 through Figure 11. Note that in all figures the plots are intentionally truncated at 400°F; this is a generally accepted and reasonable lower temperature limit for HTHA to occur.
From review of Figure 6 through Figure 11, it can be difficult to make out what the specific cut-off pressures are for each time. It turns out when these values are plotted vs. time a simple power law is obtained, which is shown in Figure 12 for Carbon Steel. The same power law relation holds for the C-0.5Mo results as well, which gives a convenient way to rapidly determine for any specific duration whether HTHA is a concern or not.
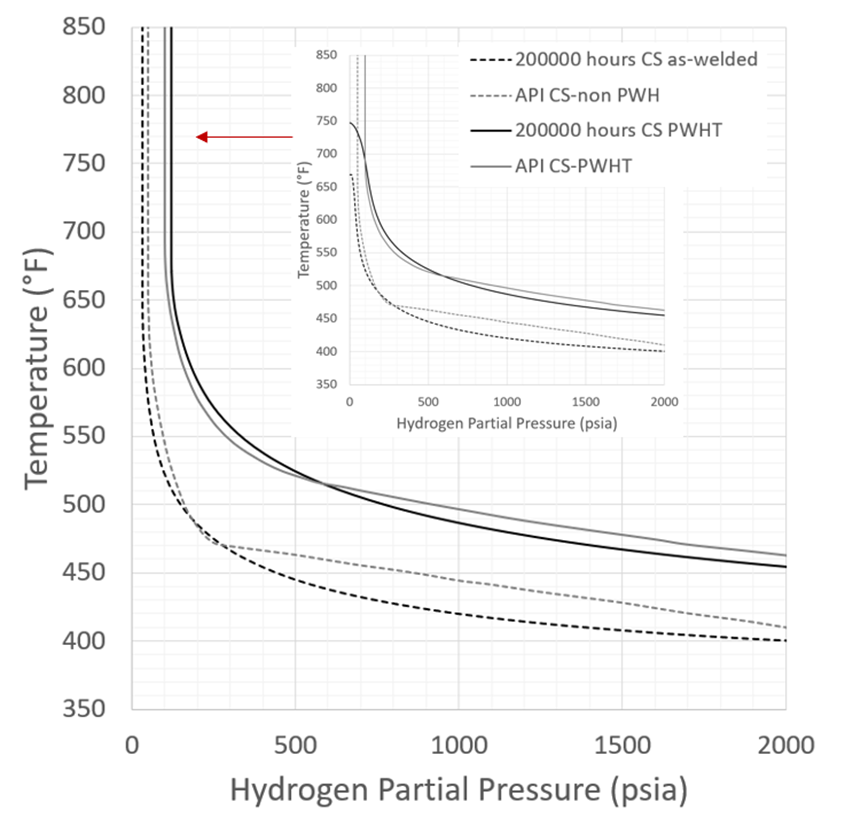
Figure 5 – Updated Carbon Steel 200,000 Results Comparison with Current API RP 941
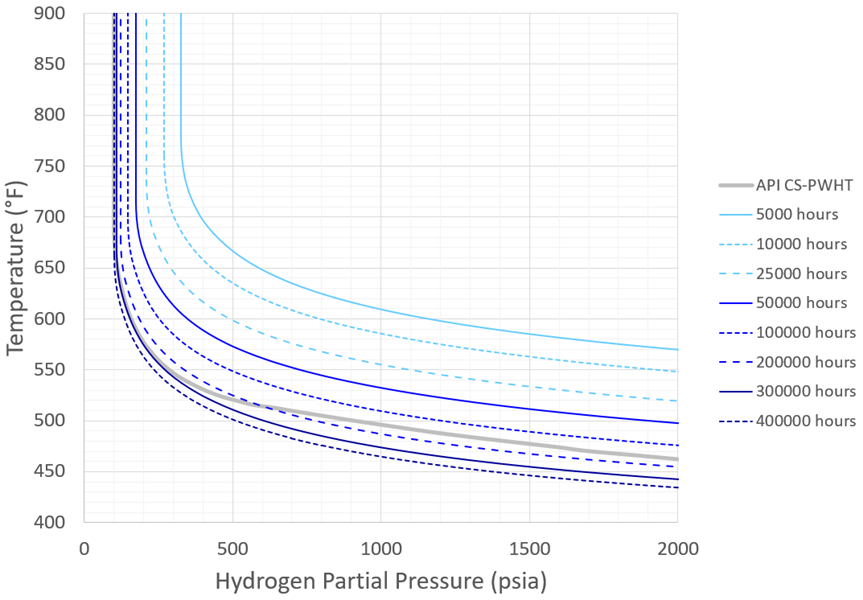
Figure 6 – Recommended Carbon Steel Nelson Curves: PWHT
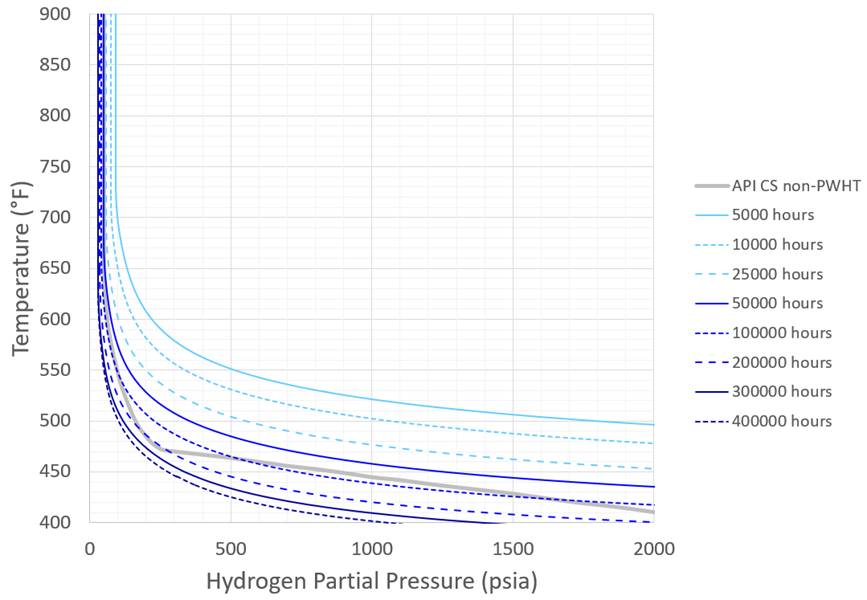
Figure 7 – Recommended Carbon Steel Nelson Curves: As-Welded
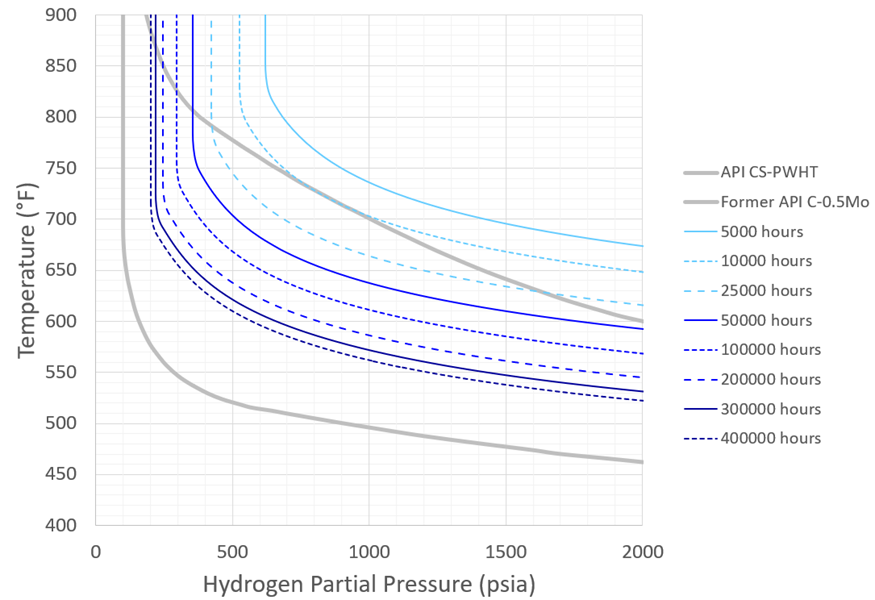
Figure 8 – Recommended C-0.5Mo Nelson Curves: PWHT, Average Performance
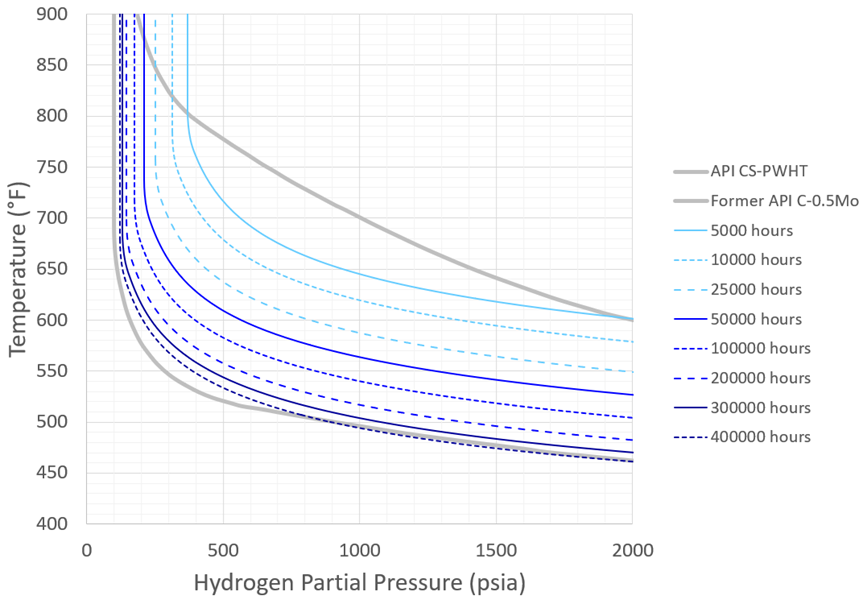
Figure 9 – Recommended C-0.5Mo Nelson Curves: PWHT, Minimum Performance
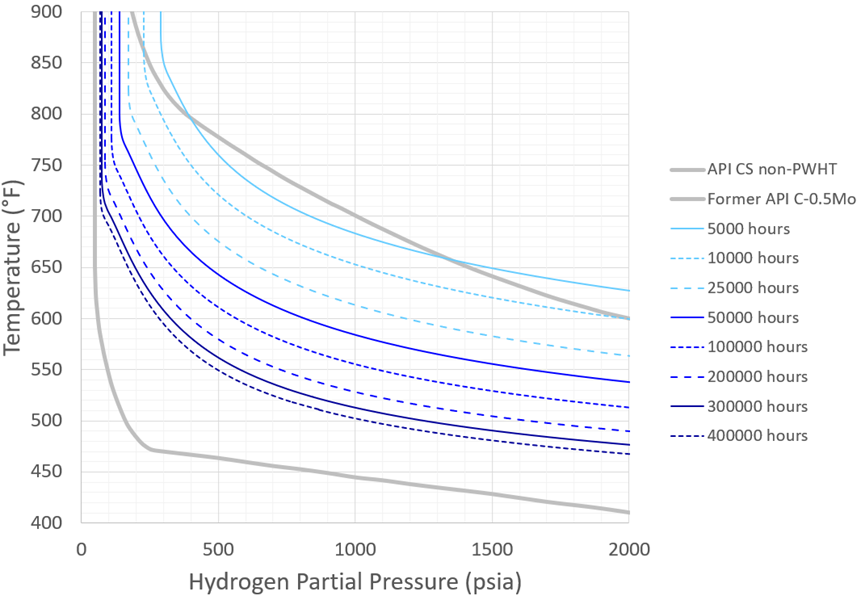
Figure 10 – Recommended C-0.5Mo Nelson Curves: As-Welded, Average Performance
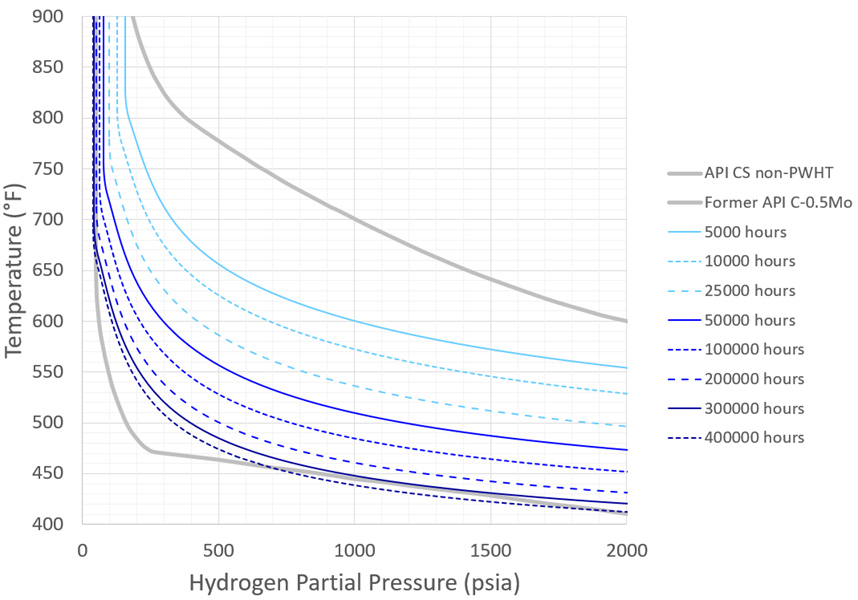
Figure 11 – Recommended C-0.5Mo Nelson Curves: As-Welded, Minimum Performance
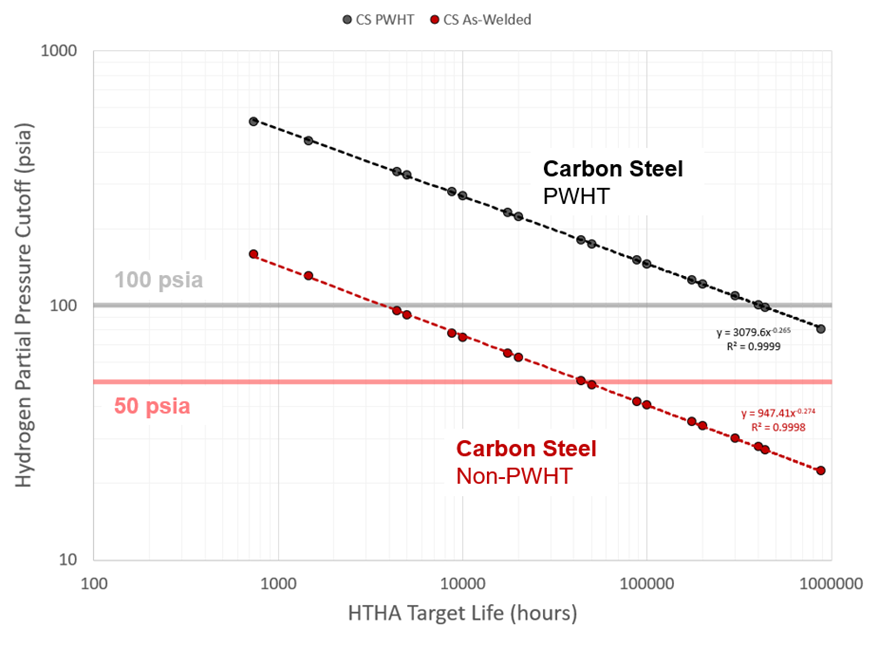
Figure 12 – Carbon Steel Cut-Off Pressures Predicted by Model
Conclusion
This blog has presented nucleation theory and its implementation as a simple driving force threshold below which HTHA cannot occur. This results in a straightforward way to remove creep effects from the model predictions; this means that creep may well need to be considered at low partial pressures and high temperatures which would be done separately from these curves. It’s also worth noting that although lower bound failure curves (failure in the through-wall or loss of containment sense) are presented in Figure 6 through Figure 11, a user-applied design or in-service margin should be incorporated when using these curves (for example a 25°F downward shift which imposes a significant safety factor on life for inspection and component life cycle planning purposes).
While the chosen nucleation-based threshold value is physically reasonable and gives logical results, it should also be kept in mind that the surface tension constant in the sintering stress term may vary substantially from typical published values – in this way the result is really semi-empirical. This does not make the results any less useful, however, as balancing theory with usability is considered a strength of our model.
References
- Dewees, D., G. Buchheim, J. Staats and C. Becht V, “Practical HTHA Experience and Time-Based Nelson Curves for Improved Equipment Life Management,” Inspectioneering, V(26)-2. March/April 2020.
- API Recommended Practice 941, “Steels for Hydrogen Service at Elevated Temperatures and Pressures in Petroleum Refineries and Petrochemical Plants,” Eighth Edition, February 2016. The American Petroleum Institute.
- API 579-1/ASME FFS-1, Fitness-For-Service, 3rd Edition, The American Petroleum Institute, 2016.
- API Standard 530, “Calculation of Heater-tube Thickness in Petroleum Refineries,” Seventh Edition, April 2015. The American Petroleum Institute.
- Shewmon, P. G., “Hydrogen Attack of Carbon Steels,” Metallurgical Transactions A, Volume 7a. February 1976.
- Raj, R. and M. F. Ashby, “Intergranular Fracture at Elevated Temperature,” Acta Metallurgica, Volume 23. June 1975.
- Raj, R., H. M. Shih and H. H. Johnson, “Correction to: ‘Intergranular Fracture at Elevated Temperature’” Scripta METALLURGICA, Volume 11.
Have questions about your HTHA impacts? Contact Becht to speak with an expert.





