Recent Advances in Becht’s HTHA Damage Modeling Approach -Part 1
Overview
This past spring, we described how we’ve incorporated well-established void growth modeling into our high temperature hydrogen attack (HTHA) assessment approach [1]. The purpose of this extension was to blend a reliable time basis for HTHA with our existing critical factor-based method (also published in the Inspectioneering Journal 6 years earlier [2]).
The Inspectioneering article was an initial step to demonstrate that existing void growth models and constants could closely reproduce the API RP 941 [3] Nelson Curves while providing a logical time-basis. Subsequent work has focused on extension and validation to the large amount of available case histories and experimental results so that the following can be characterized:
- Applied stress effects
- Through-wall damage progression
This is the first in a series of blogs that will present these advances and their extensive validation, ending with time-based Nelson Curves for Carbon Steel (CS) and C-0.5Mo suitable for inclusion in API RP 941.
Applied Stress Effects
Recall that the void growth model consists of diffusional and creep terms, where the methane pressure inside the voids is the primary driving force. To incorporate applied stress effects (such as stress in the wall due to the vessel being pressurized or welding residual stress), the following is done (identical to the description in [1]):
(Peff)diff = PH2 + PCH4 + (σ1)
(Peff)creep = PH2 + PCH4 + ( σ1 + σ2 + σ3 ) / 3
The diffusional driving force term (Peff)diff is increased by the maximum principal stress (σ1) due to all applied loadings because it’s the local stress normal to the grain boundary that drives the diffusional processes. On the other hand, the creep driving force term (Peff)creep uses the “equivalent pressure stress” due to the applied loadings, (σ1 + σ2 + σ3) / 3, also known as the hydrostatic stress, since pressure drives void growth for the creep mechanism(s).
For illustration the original curves presented in [1] are modified here to include 100% of the allowable stress as well as weld residual stresses (PWHT and as-welded). As-welded weld residual stresses (WRS) are defined as minimum yield at temperature plus 10 ksi and PWHT WRS values are taken as 30% of the full as-welded value both per API 579-1 [4]. These values are applied to both σ1 and σ2 for simplicity. Allowable stresses are assumed due to vessel pressure and also vary with temperature, with σ1 taken as the full allowable and σ2 assigned one half that value (i.e. for a cylindrical vessel). The incremental results of these additions for SA-516 Gr. 70 and 200,000 hours are shown in Figure 1.
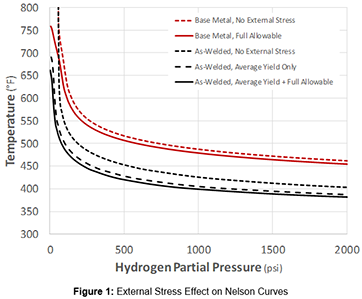
As shown in the figure, when there is applied (or “external”) stress there is no longer a pressure cutoff as hydrogen partial pressures approach zero; this physically represents creep failure in the given time for the given applied stress. That is, the vertical portion of the Nelson Curve is truncated or removed. Recall that the void growth models were first proposed for modeling creep cavitation and failure ([5],[6],[7]) such that the model does (at least theoretically) smoothly transition to the case of pure creep in the absence of hydrogen. The specific values predicted have not been harmonized against actual creep data (which is planned in the near future) but give reasonable and generally conservative zero-pressure temperatures.
Also note in Figure 1 that an alternate treatment of welds from that described in [1] is used based on the detailed calibration described in subsequent blogs. Here, CS welds are represented by a lower creep exponent as well as an enhancement to the lower temperature creep diffusivity term (based on expected increased dislocation density for welded material). Otherwise, all basic equations and constants remain the same as in [1] and are taken directly from the open literature.
The simple applied stress treatment just described gives a physically-based first approximation of stress state effects, largely enabled by the form of the void growth models themselves. In the end, the treatment is validated by the ability to reasonably predict the large set of industry data and experience which is the subject of subsequent blogs.
Through-Wall Damage Progression
The other primary extension to the model is consideration of through-wall damage. In [1] (and in Figure 1 of this blog) “failure” was taken as x = 0.5, or when void growth has consumed half the ligament between voids (see Figure 2). While x = 0.5 does represent local failure of a ligament between voids (or “fissuring”), it does not represent failure of a component or even perceptible loss of properties over a given volume of material. Rather, fissuring continues to progress on susceptible grain boundaries as well as link-up past this initial single ligament failure before property loss occurs. This is illustrated in Figure 3.
As a simple approximation, calculated void growth is allowed to continue all the way to x = 1 in an effort to capture the stages of damage past isolated fissuring. This turns out to be very effective in matching detailed through-wall damage progression documented in [8], which is presented in detail in the next blog. This simple extension allows a physical interpretation for expected damage based on the model predicted damage value (where damage is now directly equal to x), which provides a direct tie to inspection; that is, inspection results can set the starting value of damage for forward-looking predictions, and damage predictions can be described in terms of expected inspection findings.
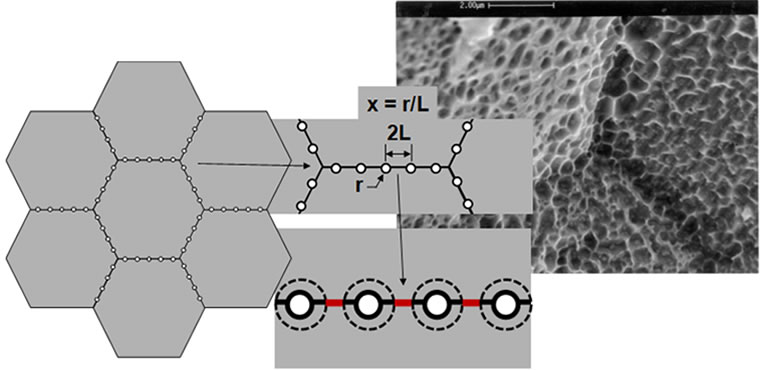
(SEM image from Reference [8])
Figure 2: Idealized Void Growth Models and Failure Criterion

(Images from Reference [8])
Figure 3: Progression of HTHA Damage
Summary
This blog has described two extensions (applied stress and through-wall damage progression) to the basic model presented earlier this year in the Inspectioneering Journal [1]. With this baseline, further development and detailed validation of through-wall damage predictions are presented in the next blog, followed by application of the model to the entire API RP 941 CS and C-0.5Mo databases and finally presentation of time-based Nelson Curves suitable for use by industry.
References
- Dewees, D., G. Buchheim, J. Staats and C. Becht V, “Practical HTHA Experience and Time-Based Nelson Curves for Improved Equipment Life Management,” Inspectioneering, V(26)-2. March/April 2020.
- Buchheim, G. “A new practical method for prioritizing equipment in HTHA service for inspection and replacement and the challenges in obtaining process conditions to be used in the HTHA Assessment,” Inspectioneering, V(20)-6. November/December 2014.
- API Recommended Practice 941, “Steels for Hydrogen Service at Elevated Temperatures and Pressures in Petroleum Refineries and Petrochemical Plants,” Eighth Edition, February 2016. The American Petroleum Institute.
- API 579-1/ASME FFS-1, Fitness-For-Service, 3rd Edition, The American Petroleum Institute, 2016.
- Hull, D. and D. E. Rimmer, “The Growth of Grain-Boundary Voids Under Stress,” Philosophical Magazine, Volume 4, No. 42. 1959.
- Raj, R. and M. F. Ashby, “Intergranular Fracture at Elevated Temperature,” Acta Metallurgica, Volume 23. June 1975.
- Raj, R., H. M. Shih and H. H. Johnson, “Correction to: ‘Intergranular Fracture at Elevated Temperature’” Scripta METALLURGICA, Volume 11.
- “Fundamental Studies of Hydrogen Attack in C-0.5Mo Steel and Weldments,” P.Lui, C. Lundin and M. Prager, Welding Research Council Bulletin 570. Welding Research Council, Inc., Shaker Heights, Ohio.
To gain more insight into this process or request information, please contact Gerrit Buchheim in the Corrosion and Materials (Pono) Group by clicking below:





