Mixing with Reaction; Practical Considerations

“My reaction is done in a few seconds; therefore, I can’t have a mixing problem.”

Mixing experts hear this frequently, but is it true?  Actually, because the reaction is fast, mixing is more likely to affect the reaction rate. However, to more fully address the question, imagine a reaction takes 10 seconds to complete. Is that fast? A mixing SME will always say “it depends”. If the mixing time (i.e. the time to 99% homogenization) is 0.1 second, then 10 seconds is a slow reaction. If the mixing time is 10 minutes, then 10 seconds is a fast reaction.

Figure 1 to the right shows a 20-gallon stirred tank with a stirring configuration requires 30 seconds for homogenization of a fluorescent dye. A reaction that quenched the dye with intrinsic timescale of 0.1 seconds also took 30 seconds to complete the quench over the full 20 gallons. An uninformed observer would conclude the reaction rate takes 30 seconds to complete and perhaps grossly overdesign a scaled-up reactor system.  In reality, the observer gained absolutely no information on intrinsic kinetics.

As another example, the neutralization of a strong acid with a strong base in an aqueous medium is known to be essentially “instantaneous.”  The reaction time is less than a picosecond, on the order of hundreds of femtoseconds, and is estimated only with great effort [1, 2]. According to transition state theory [3], the fastest that a reaction event can occur (zero activation energy) is 160 fs at 300 K.

However, below in Figure 2 is an example of an acid-base neutralization in miscible fluids attempted in a viscous media, where yellow zones are locations where the neutralization reaction has occurred:

Figure 2.  Time sequence of a strong acid -strong base reaction in a stirred viscous medium

The liquid volume is < 500 mL here.  This “instantaneous chemistry” isn’t completed even within 10 minutes, in this case due to low velocity in portions of the volume, systematic unmixed zones that can occur in stirred laminar stirred flow [4, 5], and relative slowness of molecular diffusion.  There are a number of pitfalls that can result from this experiment:

1. The measured (apparent) reaction rate is many orders of magnitude slower than the intrinsic reaction rate.
2. False predictions for scale-up are certain. For instance, the impeller Reynolds number always increases upon scale-up, into a regime where the systematic unmixedness may not occur.
3. How and where the feed is introduced is important.
4. How and where samples are taken is important.
5. Non-stoichiometric regions will exist!

Hence, the net reaction rate and selectivity could be impacted, perhaps leading to overdesign or even abandonment of the project altogether.

The upshot is that the measured reaction rate is the maximum of:  the intrinsic reaction time, the mixing time, and, for multiphase reactions, related to the film diffusion time. For this reason, intrinsic kinetics are measured at very small scales, as in a stopped-flow apparatus [6].  The mixing is designed to occur at millisecond scales, faster than the regime of many reactions of interest.  The mixing time is a well-characterized and known limit of the device.  Thus, any reaction timescale getting close to the stopped-flow mixing time is suspected to not represent fully intrinsic kinetics.

Why do we care?  Unless the mixing affects the reaction selectivity, we may not care at all. For a single reactant, mixing doesn’t have much if any effect.

A –> C

The “A” reacts in a first order decay, completely unaware of its surroundings, albeit limited heat dissipation that accompanies poor mixing may affect measured kinetics.

For second order reactions, like

A + B –> C

there is perhaps a mixing impact.  Suppose our reaction is that of hydrochloric acid and sodium hydroxide in water.  The reaction product is only sodium chloride and more water, nothing else.  There are no selectivity considerations. The only reason we care about the neutralization rate is that we may not want unreacted strong acid or base contacting the internals of a vessel or a pipe wall.  The aforementioned heat dissipation could also be a consideration.

Now suppose we have reaction of the form below, where both desired and undesired reaction products are possible:

A + B –> R     (desired, rate constant k₁)
R + B –> S      (undesired, rate constant k₂)

Examples are where species A can have multiple reacting sites for B, or where there are oligomerization reactions that can occur.  If the reaction to make R is much faster than the second reaction, we intuitively expect that we will make mostly R.  If the mixing is also much faster than the reactions, we will indeed make R as shown in Figure 3 below as a limiting case. Note τ_m is the mixing timescale and τ_R is the reaction timescale.

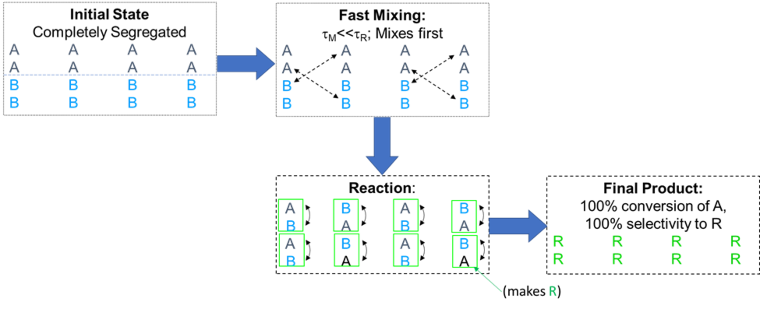
Figure 3.  Limiting case: Reaction sequence when mixing is much faster than reaction

However, now imagine the case where the mixing is much slower than the “fast” reaction.  See Figure 4.  The A and B will react near the interface of the unmixed blobs of A and B, making product R that is still at the interfacial blob.  At this point, the R can only react with more B to make undesired S.  The limiting result is that the fast reaction makes only S and with only 50% conversion of A.  The chemist and engineer would truly be scratching their heads at this result.

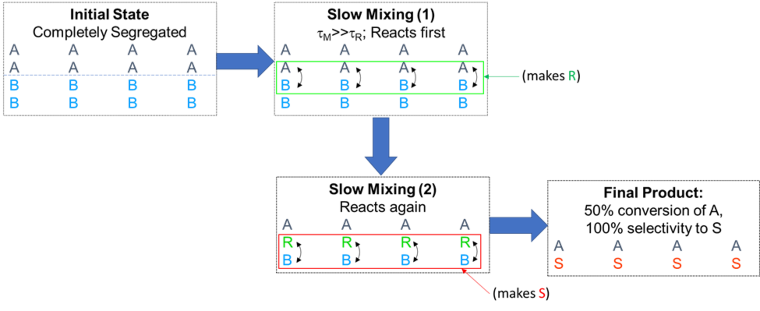
Figure 4.  Limiting case: Reaction sequence when reaction is much faster than mixing

In reality, the system will give a product distribution between the two limits shown in Figure 3 and Figure 4. The rate laws can be integrated for the well-mixed case.

A selectivity parameter X_S is defined based on the balance of species A to characterize reactor performance:

X_S = 2[S] / ([R] + 2[S])

where the squared brackets represent concentration of the species R and S at the end of the reaction or exit of the reactor.  The X_S is bounded 0 to 1.

Damköhler numbers (Da) are used to characterize systems in which competing timescales are important to a system.  For mixing and reacting systems we use

Da= τ_m/τ_R

Alternately, we can think in terms of rates; the mixing rate is 1/τ_m and the reaction rate is 1/τ_R.  For Da > 1, mixing sensitivity on the reaction needs to be considered. The observed selectivity X_S is a function a function of both Da and the ratio k₁/k₂ [7].

For a second order reaction, the timescale can be taken as the inverse of the second order rate constant multiplied by the initial concentration of the limiting reagent.  From a pseudo-first order perspective, it can be thought of as similar to the half-life of the limiting reagent.

There are various methods to calculate the mixing timescale τ_m for turbulent flow.  For mixing at the smallest scales (micromixing), it is dependent on the length scale of the smallest turbulent eddies (the so-called Kolmogorov length scale) divided by the diffusion coefficient of the reactant being mixed [8].  The Kolmogorov length scale is related to the kinematic viscosity and power input to the fluids.

Laminar mixing is based on the folding and stretching of individual lamella and then diffusion between them [9].  Instantaneous reactions occur at the interface of the individual lamella while slower reactions create concentrations profiles across the lamellae. The rate of laminar mixing is not necessarily affected appreciably by reactions.

Figure 5, below, shows roughly what a mixing SME would consider slow vs. fast vs. instantaneous chemistry in terms of the reaction timescale, based on what is practical for mixing timescale in turbulent conditions.

Figure 5.  Reaction time scales with real-world categorizations

For slow reactions, τ_R >> τ_m, and mixing occurs before significant reaction. Bulk or average concentration, temperature, etc. are sufficient to predict reactor performance.

At the opposite extreme, we have instantaneous reactions with τ_R << τ_m, and the reaction zone is very small and localized, such as near the feed point of B.  Mixing will limit the rate of chemical reaction and determines selectivity.  The observed reaction rate is actually the mixing rate.

In between, we have fast reactions with τ_R ~ τ_m.  Mixing and reaction occur at approximately the same rate.  Mixing will generally affect the rate of chemical reaction rate and selectivity, however it is sometimes possible to design a mixing system to minimize byproduct formation [10].

In the author’s experience, for large scale industrial mixing (thousands of gpm for each flow with a pressure drop on the order of 10 psi), the lowest practical mixing timescale is 0.1 s for an inline design.  As stated earlier, a lab stopped-flow reactor can mix on the order of 0.001 s.  Hence there is a scale affect, as we know intuitively that reactants must travel farther distances to mix as scale increases.

Stirred reactors have much larger mixing timescales than do inline mixers such as static mixers.  Stirred reactors of 1000 gallon volume, for instance, commonly have mixing timescales near a minute.  Stirred vessels are sometimes required, as in semi-batch reactors, because reactants and other materials are added in sequence to meet a given formulation target. There are mixing “tricks” to minimize byproduct formation, such as slow addition rate, diluted additive, and feed near an impeller, i.e. the highest power zone.

Tools

Ideally, we know the chemical kinetics and can estimate the system Da so that we can assess for possible mixing sensitivity. Also ideally, the chemistry can be studied at multiple process scales before a full-scale reactor is constructed and operated.  The reason for the need for multiple scales is that the mixing timescale τ_m can’t be varied over a large range in a single sized reactor.  In lab studies (< 1 liter volume), in fact, it is hard not to mix the reactants relatively fast. The mixing time will always be in the “fast” regime and can’t be varied over an order of magnitude.

If a chemistry is “severe” enough, it may not be desired to study it directly in the lab or pilot scale.  An example is chemistry involving highly toxic chemicals and/or operating in a flammable region and/or operation at high pressure and temperature.  In these cases, we turn to molecular modeling to estimate the thermochemistry and rates of reaction, and Computational Fluid Dynamics (CFD) to study the flow field with reactions.  While CFD certainly can’t mimic the smallest of scales over which molecular mixing occurs, there are tools such as Large Eddy Simulation (LES) [11] that model the scales smaller than the numerical grid for turbulent systems.

Closing Comments

The mixing considerations discussed in this blog are just a small sample of the full spectrum of reacting flows and fluid mixing.  Within the whole realm of reacting flows, beyond the scope of this blog, is the scale of mixing that limits the reaction.  There are three scales defined:

Macromixing is the distribution of reactant blobs into the vessel, and is determined by blend time and overall flow pattern.

Mesomixing is the process of making feed blobs smaller and smaller.  It is determined by local shear and energy dissipation.

Micromixing is the final stage of mixing in which molecular diffusion and reaction occur.

The mixing timescales of each of these are different. If the physical properties of the reactant streams are very different (e.g. disparate viscosity [12]), the situation is even more complex.

Feel free to contact Becht for further discussions on these topics or other topics related to inline and stirred tank mixing.

contact becht 

Further reading

Bourne, J.R., “Mixing and the Selectivity of Chemical Reactions”, Org. Process Res. Des. Dev., 2003, 7(4) pp. 471-508.

Bałdyga, J., Bourne, J.R., Hearn, S.J., “Interaction between chemical reactions and mixing on various scales”, Chem. Eng. Sci., 1997, 52(4), pp. 457-466.

References

1. Rini, M., Pines, D., Magnes, B.-Z., Pines, E., Nibbering, E.T.J., “Bimodal proton transfer in acid-base reactions in water”, Chem. Phys., 2004, 121, pp. 9593 – 9610.
2. Hassanali, A., Prakash, M.K., Eshet, H., Parrinello, M., “On the recombination of hydronium and hydroxide ions in water”, Proceedings of the National Academy of Sciences, 2011, 108, pp. 20410 – 20415.
3. Glasstone, S.; Laidler, K. J.; Eyring, H., Theory of Rate Processes; McGraw-Hill: New York, 1941.
4. J. Lamberto, M.M. Alvarez, F.J. Muzzio, “Experimental and computational investigation of the laminar flow structure in a stirred tank”, Chem. Eng. Sci., 1999, 54(7), pp. 919-942.
5. Szalai, E.S., Alvarez, M.M., Muzzio, F.J., “Laminar Mixing: A dynamical systems approach” chapter in Handbook of Industrial Mixing: Science and Practice, Paul, E.L., Atiemo-Obeng, V.A., Suzanne M. Kresta, S.M., eds., pp. 89 – 143, John Wiley & Sons, 2003.
6. https://en.wikipedia.org/wiki/Stopped-flow
7. Patterson, G.K., Paul, E.L., Kresta, S.M., Etchells III, A. W. , Mixing and Chemical Reactions chapter in Handbook of Industrial Mixing: Science and Practice, Paul,E.L., Atiemo-Obeng, V.A., Suzanne M. Kresta, S.M., eds., pp. 755-867, John Wiley & Sons, 2003.
8. Bałdyga, J., Bourne, J.R., Turbulent Mixing and Chemical Reactions, John Wiley & Sons, 1999.
9. Szalai, E.S., Kukura, J., Arratia, P.E., Muzzio, F.J., “Effect of Hydrodynamics on Reactive Mixing in Laminar Flows”, AIChE J., pp. 168 – 179, 49(1), 2003.
10. Bachman, G.W., Jones, R.M., Cloeter, M.D., Lipp, C.W., Bartel, M.J., Coomes, B.J., Daigle, S.J., Janda, S.F., “Mixer for Continuous Flow Reactor”, US9700855B2.
11. Pope, S.B., Large Eddy Simulation chapter in Turbulent Flows, 558 – 639, Cambridge University Press, 2000.
12. Pathikonda, G., Usta, M., Ahmad, M.C., Khan, I., Gillis, P., Dhodapkar, S., Jain, P., Ranjan, D., Aidun, C.K., “Mixing behavior in a confined jet with disparate viscosity and implications for complex reactions”, Chem. Eng. J., 2021, 403, p. 126300.