Continuum Damage FEA Implementation of the Becht HTHA Model
With contributing authors Scott Leakey, Dave Dewees, P.E.
It’s approaching three years since we demonstrated a mechanistic model for high-temperature hydrogen attack (HTHA). The model is fundamentally based on void growth and captures both mass-diffusion as well as power-law creep mechanisms which are responsible for the growth and eventual linking of internal cavities. A six-part series on the mechanics of the model has already been presented – you can find the first part here. More recent enhancements, including the inclusion of weld residual stresses, nucleation effects, C-0.5Mo material, and validation of through-wall damage predictions over close to 100 case histories, can be found here.
Modelling HTHA requires several inputs, some of which are not always known or easily calculated by hand. Temperature, hydrogen partial pressure, applied (and residual) stress, for example, all affect damage rate and often vary with position and (especially in the case of stress) even time. In all but the simplest component geometries, these spatial and temporal variations become increasingly difficult to predict with closed-form solutions. Assessment of more complex three-dimensional components lends itself perfectly to finite element analysis (FEA), where the thermal, hydrogen partial pressure, and stress distributions within the component are readily obtained through heat transfer, mass diffusion, and viscoelastic stress analyses, respectively. Since development on the HTHA modeling began, it has always been the intent to use the power of FEA to accurately capture HTHA damage in conditional assessments of in-service equipment where geometric complexities were previously limited to simplifying 1D assumptions.
For the first time, the Becht HTHA model has been applied within the sequential coupled multi‑physics finite element analysis methodology described above, through the use of a custom creep user subroutine developed for the commercial analysis software package, ABAQUS. The subroutine calculates HTHA damage accumulation throughout a quasi‑static stress analysis resulting in a three-dimensional progression of the damage field that may be used to inform risk calculations, remaining life assessments, and inspection recommendations. The analysis has been conducted as a benchmarking study against a seminal paper [1] in the field, in which damage accumulation in a pressure vessel nozzle was simulated and later verified through destructive examination.
The Details
The HTHA model uses the CREEP user subroutine available in ABAQUS. State-dependent variables (SDVs) are used to track the HTHA damage fraction element integration points, along with other variables such as methane pressure, diffusion rates, local creep rates, hydrogen partial pressure, and principal stresses.
Hydrogen partial pressure distribution through the component wall is not specified but rather solved for directly through a mass-diffusion analysis and application of the Sievert Law. This is particularly important for configurations that involve regions of complex geometry which promote three-dimensional diffusion effects.
Temperature and partial pressure variation over time can be captured directly, which is a valuable technique for complex time histories. The approach may also be combined with a transient assessment in Becht’s 1D HTHA tool to generate an estimate of the “damage equivalent” steady-state operating conditions which can then be adopted as a single analysis case in the FEA.
At this time, coupling of the damage field with the diffused hydrogen and temperature fields is only possible on a sequential basis, meaning that changes to the underlying pressure distribution as material becomes fully damaged—with higher partial pressures allowed to penetrate through the damaged material—are currently not accounted for without sequential iteration. Exploration into coupling these fields together is planned in the future.
Comparison and Verification
In a paper presented at the ASME Pressure Vessels & Piping Conference in 2020 [1], Bagnoli et al of EMRE described a continuum damage mechanics (CDM) approach to HTHA modelling based on ductility exhaustion. The model included strain effects due to both HTHA as well as traditional creep phenomena. The strain rate based on HTHA damage was essentially an empirical relationship based on published dilatometry experiments [2, 3, 4, 5]. As verification, the authors modelled HTHA damage progression in an inlet nozzle of a hydroprocessing unit, which was then destructively examined. Good agreement was found between the modelled and detected HTHA damage.
Some significant differences are observed between the Becht and EMRE models. Although the HTHA creep strains are used in the calculation of the damage measure, the Becht model does not use ductility exhaustion as a means of quantifying failure. Becht’s failure criterion is based on correlation between macroscopic structural damage and toughness loss in comparison to a grain boundary void growth damage parameter. The way damaged material reacts is also different – in the Becht model, damaged material observes a corresponding reduction to elastic modulus, which is common to the EMRE work, but is significantly less severe by comparison. Given these differences in approach, it was expected that some differences in results would be observed, but given the good experimental validation, we decided to analyze the exact same nozzle under the same conditions to see how the Becht model would perform.
The nozzle in question is shown in Figure 1 and the geometry was extracted from the original analysis with the generous assistance of EMRE. The 2D axisymmetric model includes the nozzle itself along with a sufficient portion of the vessel head to limit boundary effects. The model also includes a type-347 weld overlay along the internal wetted surface.
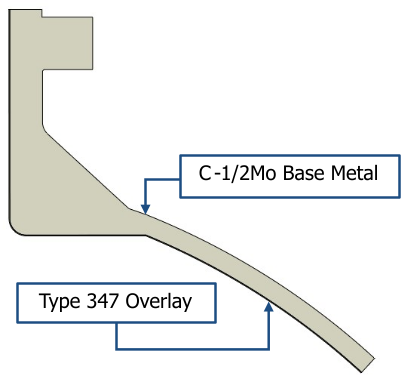
Figure 1. Nozzle geometry
A constant isothermal temperature distribution of 400 °C (752 °F) was assumed in the EMRE model and replicated in our analysis. For establishing the thru-wall hydrogen partial pressure distribution, both approaches included a mass-diffusion analysis. Given that the operating conditions (PH2 = 4.3 MPa) were identical, the geometry was identical, and the material solubility and diffusivity was derived from the same source [6], the results were unsurprisingly also identical, as demonstrated in Figure 2. An excellent example of the effect of three-dimensional diffusion is observed along the thickest pathway of the nozzle root. Presence of the overlay reduces the hydrogen partial pressure as seen by the base metal ID surface from 4.3 MPa down to 3.8 MPa at this location, while in the far field head region this reduction is more pronounced, dropping to a value of 1.5 MPa (matching 1-D hand calculations). Accounting for the effect of additional thickness at the root location, without the 3-D diffusion effects, the base metal ID would have been assumed to see just over 2.9 MPa—an underestimation of the hydrogen partial pressure of over 30%!
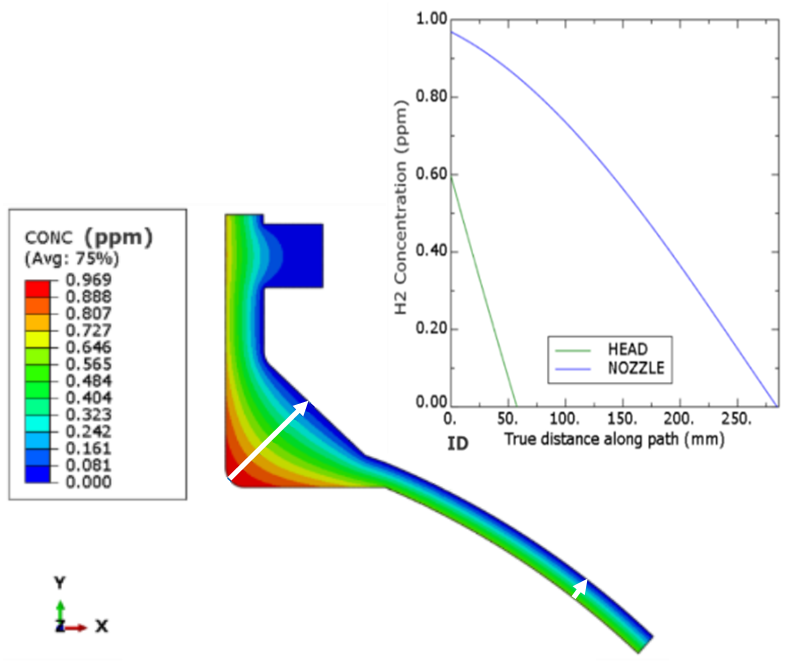
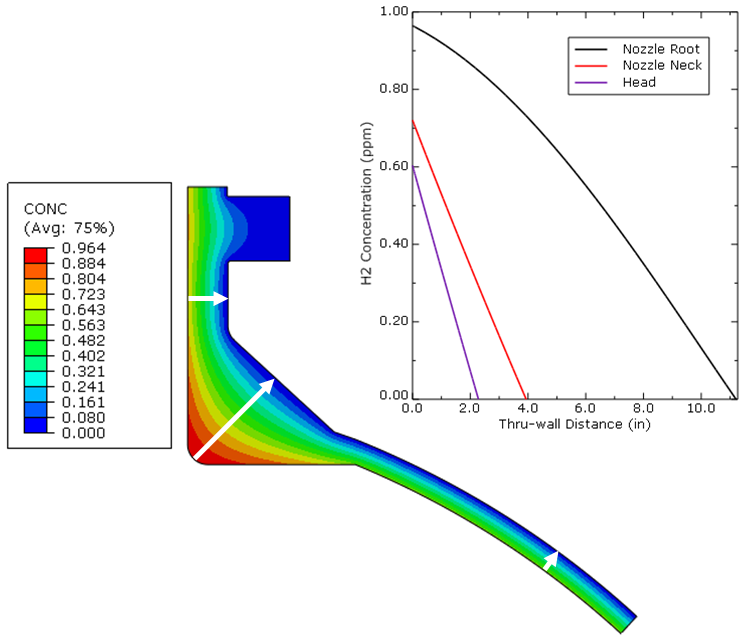
Figure 2. Comparison of calculated hydrogen partial
pressures showing identical results
There is one further thing to note before we discuss HTHA damage results. C-0.5Mo is known to be a widely variable material in terms of HTHA resistance. To account for this scatter, the Becht model includes the concept of carbon activity (ac), which describes the reactivity of the carbides in the presence of hydrogen. This is set in the range 0 to 1, where plain carbon steel exhibits an ac of 1. With the addition of carbide stabilizers, the alloy steels exhibit lower values of ac, which is responsible for their improved HTHA resistance. For the population that we have analyzed, we have found that the range 0.35 < ac < 0.75 bounds the statistical property scatter of C-0.5Mo well. For this analysis, a value of ac = 0.5 was used, i.e. close to, but slightly improved over, mean properties.
The results in terms of the calculated HTHA damage after a simulated 100,000 hours of operation are shown in Figure 3. Although failure is represented by two different concepts between the approaches—in the EMRE analysis, 5% failure strain, and in the Becht analysis, complete consumption of the ligament between voids by void growth—in both cases the scale ranges from 0 (undamaged) to 1 (full damage).
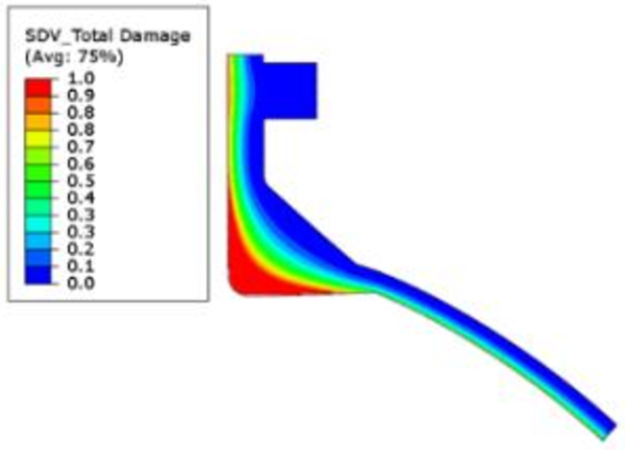
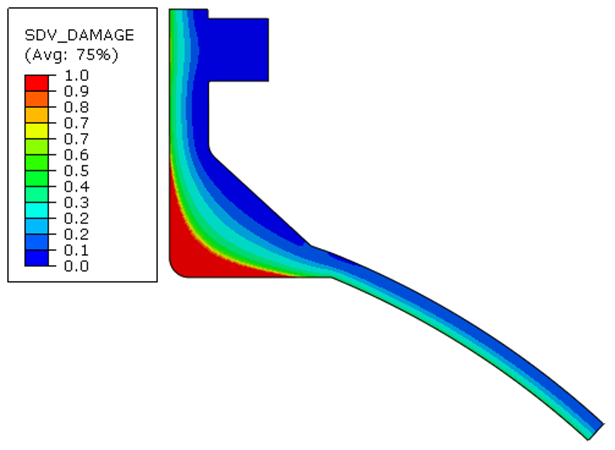
Figure 3. Results of EMRE model and Becht model after 100,000 hours
The results are remarkably similar. In both cases the damage is most severe in the internal corner as is consistent with the hydrogen diffusion analysis (Figure 2). This area has the longest diffusion pathway and is also exposed to hydrogen on both sides and therefore we expect a slower fall off of hydrogen partial pressure thru-wall. This is consistent with the damage that was observed in the destructive examination (shown in Figure 4, which is reproduced from [1]).

Figure 4. Microstructural damage observed in nozzle. Reproduced from [1]
The damage gradient is seen to be approximately equal and in the range 0.2 – 0.4 at the mid-wall in both cases. This would indicate that although HTHA damage should be observable (as indeed it was) on the internal surface, it is unlikely that complete failure of the nozzle was imminent. Damage in the flange and outer wall, and also in the head, is also seen to be very similar.
The ability to reliably model damage distribution and progression is a promising step forward for risk management in these components. The fact that the model is mechanisticly-based is also exciting from a materials science perspective – it allows us to understand the accumulation of HTHA damage at a micro-level and in doing so, better understand the ways we can mitigate risks in the future.
Conclusions
As we discussed earlier, there are some significant differences between the two approaches, but the important result is that the results are very similar. This finding does reinforce our belief that the mechanistic model we have developed is performing well in real-world comparisons. Although the finite element model shown in this example is a 2D model, 3D cases have also been run successfully using the user subroutine. There is no barrier to this kind of analysis becoming commonplace among the mechanical engineers seeking to understand and predict the condition of their equipment.
In parallel, a lot of work is ongoing simultaneously on the inspection side and we are expecting an API Recommended Practice (RP 586) on inspection for HTHA fairly soon. The coupled modelling-inspection approach is the ideal endgame; signs are positive that we as an engineering community will soon have a standardized approach to HTHA assessment with multi-level controls. We are, of course, continuing our work in this area – check out our Joint Industry Project if you haven’t already!
References
| [1] | K. E. Bagnoli, Z. A. Cater-Cyker, R. L. Holloman, C. A. Hay, L. T. Hill and K. M. Nikbin, “Volumetric Damage Modelling of High Temperature Hydrogen Attack in Steel Using a Continuum Damage Mechanics Approach,” in Proceedings of the ASME 2020 Pressure Vessels & Piping Conference (PVP2020), Minneapolis, 2020. |
| [2] | M. McKimpson and P. G. Shewmon, “Initial Hydrogen Attack Kinetics in a Carbon Steel,” Met Trans. A, vol. 12A, 1981. |
| [3] | B. Panda, “Kinetics of Hydrogen Attack in 1020 Steel,” Ph.D Thesis, Ohio State University, 1982. |
| [4] | T. A. Parthasarathy, “Kinetics of Hydrogen Attack in 2.25Cr Steel,” Ph.D Thesis, Ohio State University, 1983. |
| [5] | T. A. Parthasarathy, “Mechanisms of Hydrogen Attack of Carbon and 2.25Cr-1Mo Steels,” Acta. Metall., vol. 33, no. 9, p. 1673, 1985. |
| [6] | D. A. Osage, D. W. Spring, T. L. Anderson, S. R. Kummari, P. E. Prueter and K. R. W. Wallin, “Recommendations for Establishing the Minimum Pressurization Temperature (MPT) for Equipment,” WRC Bulletin 562, 2017. |





